LeetCode-in-Swift

Medium

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

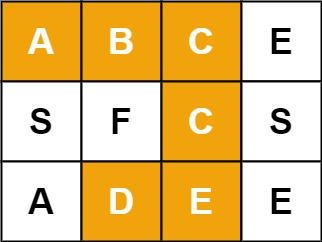
Input: board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCCED”

Output: true

Example 2:

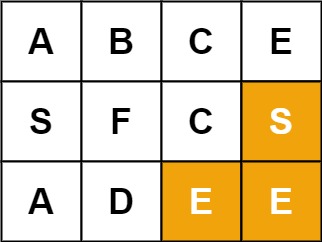
Input: board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “SEE”

Output: true

Example 3:

Input: board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCB”

Output: false

Constraints:

Follow up: Could you use search pruning to make your solution faster with a larger board?

To solve the “Word Search” problem in Swift with the Solution class, follow these steps:

  1. Define a method exist in the Solution class that takes a 2D character array board and a string word as input and returns true if the word exists in the board.
  2. Implement a backtracking algorithm to search for the word in the board.
  3. Iterate through each cell in the board:
    • For each cell, call a recursive helper function search to check if the word can be found starting from that cell.
    • If search returns true, return true immediately.
  4. Define the search method to perform the recursive backtracking:
    • Check if the current cell is out of bounds or if the current character in the board does not match the corresponding character in the word.
    • If any of the conditions are met, return false.
    • Mark the current cell as visited by changing its value to a special character (e.g., #) to avoid revisiting it.
    • Recursively call search on neighboring cells (up, down, left, right) with the next character in the word.
    • After exploring all possible paths from the current cell, backtrack by restoring the original value of the current cell.
  5. If the search method reaches the end of the word, return true.
  6. If no match is found after exploring all cells, return false.

Here’s the implementation of the exist method in Swift:

class Solution {
    func exist(_ board: [[Character]], _ word: String) -> Bool {
        
        var word = Array(word)

        var beginnings = [(Int, Int)]()

        for r in 0..<board.count{
            for c in 0..<board[0].count{
                if board[r][c] == word[0]{
                    beginnings.append((r, c))
                }
            }
        }

        var has = false
        for tup in beginnings{
            if word.count == 1{
                has = true
                break
            }

            var visitedBoard = \[\[Bool]](repeating:[Bool](repeating:false, count:board[0].count), count:board.count)
            visitedBoard[tup.0][tup.1] = true

            if proceed(tup, board, &visitedBoard, 1, word){
                has = true
                break
            }

        }

        return has

    }


    func proceed(_ startP:(Int, Int), _ board: [[Character]], _ visitedBoard:inout[[Bool]], _ targetIndex:Int, _ word:[Character]) -> Bool{

        let (r, c) = startP
        let rows = visitedBoard.count
        let cols = visitedBoard[0].count
        //try four directions
        //up
        var has = false
        if r - 1 >= 0{
            if visitedBoard[r-1][c] == false{
                if board[r-1][c] == word[targetIndex]{

                    if ((targetIndex + 1) == word.count){
                        return true
                    }

                    visitedBoard[r-1][c] = true
                    let tup = (r-1, c)
                    let res = proceed(tup, board, &visitedBoard, targetIndex+1, word)
                    visitedBoard[r-1][c] = false
                    if res == true{
                        return true
                    }
                }
            }
        }

        //left
        if c - 1 >= 0{
            if visitedBoard[r][c-1] == false{
                if board[r][c-1] == word[targetIndex]{

                    if ((targetIndex + 1) == word.count){
                        return true
                    }

                    visitedBoard[r][c-1] = true
                    let tup = (r, c-1)
                    let res = proceed(tup, board, &visitedBoard, targetIndex+1, word)
                    visitedBoard[r][c-1] = false
                    if res == true{
                        return true
                    }
                }
            }
        }

        //down
        if r + 1 < rows{
            if visitedBoard[r+1][c] == false{
                if board[r+1][c] == word[targetIndex]{

                    if ((targetIndex + 1) == word.count){
                        return true
                    }

                    visitedBoard[r+1][c] = true
                    let tup = (r+1, c)
                    let res = proceed(tup, board, &visitedBoard, targetIndex+1, word)
                    visitedBoard[r+1][c] = false
                    if res == true{
                        return true
                    }
                }
            }
        }

        //right
        if c + 1 < cols{
            if visitedBoard[r][c+1] == false{
                if board[r][c+1] == word[targetIndex]{

                    if ((targetIndex + 1) == word.count){
                        return true
                    }

                    visitedBoard[r][c+1] = true
                    let tup = (r, c+1)
                    let res = proceed(tup, board, &visitedBoard, targetIndex+1, word)
                    visitedBoard[r][c+1] = false
                    if res == true{
                        return true
                    }
                }
            }
        }

        return false
    }
}

This implementation uses backtracking to search for the word in the board, with a time complexity of O(M * N * 4^L), where M and N are the dimensions of the board and L is the length of the word.

This site is open source. Improve this page.