LeetCode-in-Swift

124. Binary Tree Maximum Path Sum

Hard

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node’s values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

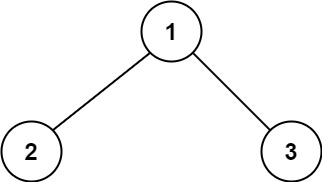
Input: root = [1,2,3]

Output: 6

Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

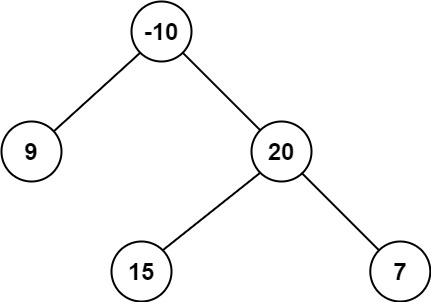
Input: root = [-10,9,20,null,null,15,7]

Output: 42

Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 104].
• -1000 <= Node.val <= 1000

To solve the “Binary Tree Maximum Path Sum” problem in Swift with a Solution class, we’ll use a recursive approach. Below are the steps:

1. Create a Solution class: Define a class named Solution to encapsulate our solution methods.

2. Create a maxPathSum method: This method takes the root node of the binary tree as input and returns the maximum path sum.

3. Define a recursive helper method: Define a recursive helper method maxSumPath to compute the maximum path sum rooted at the current node.
   • The method should return the maximum path sum that can be obtained from the current node to any of its descendants.
   • We’ll use a post-order traversal to traverse the tree.
   • For each node:
     • Compute the maximum path sum for the left and right subtrees recursively.
     • Update the maximum path sum by considering three cases:
       1. The current node itself.
       2. The current node plus the maximum path sum of the left subtree.
       3. The current node plus the maximum path sum of the right subtree.
     • Update the global maximum path sum if necessary by considering the sum of the current node, left subtree, and right subtree.

4. Initialize a variable to store the maximum path sum: Initialize a global variable maxSum to store the maximum path sum.

5. Call the helper method: Call the maxSumPath method with the root node.

6. Return the maximum path sum: After traversing the entire tree, return the maxSum.

Here’s the Swift implementation:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public var val: Int
 *     public var left: TreeNode?
 *     public var right: TreeNode?
 *     public init() { self.val = 0; self.left = nil; self.right = nil; }
 *     public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }
 *     public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {
 *         self.val = val
 *         self.left = left
 *         self.right = right
 *     }
 * }
 */
public class Solution {
    private var maxSum = Int.min

    private func helper(_ root: TreeNode?) -> Int {
        guard let root = root else {
            return 0
        }

        let left = max(0, helper(root.left))
        let right = max(0, helper(root.right))
        let current = root.val + left + right
        maxSum = max(maxSum, current)

        return root.val + max(left, right)
    }

    public func maxPathSum(_ root: TreeNode?) -> Int {
        _ = helper(root)
        return maxSum
    }
}

This implementation follows the steps outlined above and efficiently computes the maximum path sum in a binary tree in Swift.

This site is open source. Improve this page.